こんにちは。謎解きブロガーのハルです。
【謎解きの作り方】シリーズでは、「謎解きは誰でも作れる！」をコンセプトに「謎解きの作り方」を紹介しています。
今回のテーマは「覆面算」です。
- 自分で謎解きを作ってみたい人
- 謎解きのネタを探している人
- もっとお手軽に謎を作りたい人
後半には練習パートもあるので、一緒に謎解きを作っていきましょう。
また「私は謎解きを作るより、解くほうが好きだよ」という人も「謎解きの作り方を知ること」＝「謎解きのパターンを知ること」につながります。
より「謎解き力を高めたい」という人にも参考になる記事となっているので、是非ご一読ください。
１．「覆面算」とは？
まずは今回のテーマである「覆面算」とは何かについて簡単にお伝えします。
「覆面算」とは、「０から９までの数字を文字（または記号）に置き換えた計算式」のことです。つまり、数字が隠されている（＝覆面）計算式のことを指します。
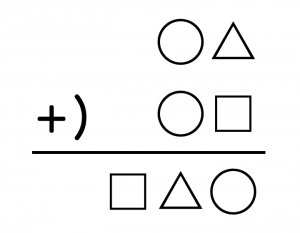
どの数字にどの文字（または記号）が対応しているかを考えながら解いていきます。
「覆面算」といえば、概ね「足し算の筆算」の形式を指すことが多いですが、中には「複数の式を並べる（連立方程式のような）覆面算」もよく使われます。
謎解きでは、計算結果がそのまま答えになったり、文字と数字の対応表を作らせたりなどといった使われ方があります。
２．「覆面算」の作り方
「覆面算」の作り方を紹介する前に、ある有名な覆面算の問題を一つ出題します。
ここで解いてもよいですし、大変そう…と思った人は飛ばしていただいて大丈夫です。
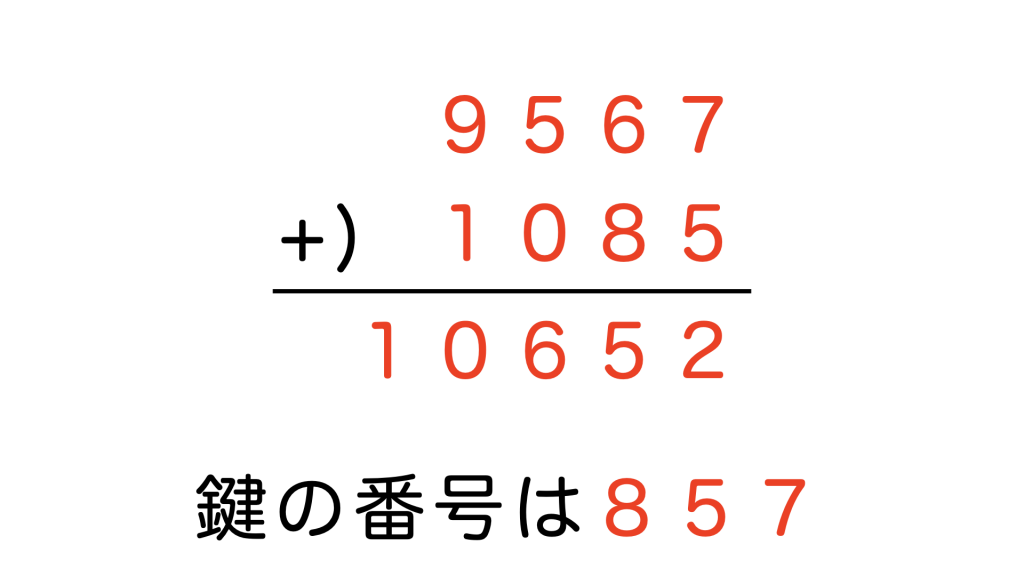
これはイギリスのパズル作家・数学者であるデュードニー氏が作ったもので、「SEND MORE MONEY（もっと金を送れ）」という意味のある単語で作ったはじめての覆面算とされています。
今回は謎解き風に、これを解けば「鍵の番号が分かるよ」みたいな感じで、鍵の番号も「RED（＝赤）」という単語になるようにアレンジしてみました。
こんな感じに意味のある単語で自作するのは中々大変ですが、基本的には「数字」を「文字・記号」に変換しても解くことができれば、それが「覆面算」です。
ただ「計算は苦手だよ〜」「作るの難しそう…」という人のために、ここではとても簡単に覆面算を作るための「便利なサイト」および「気をつけたいこと」をお伝えしていきます。
①便利なサイト
まずは、覆面算を作るために便利なサイトを紹介します。
Cryptarithm Solver
海外のサイトですが、加減乗除（+-×÷）すべての計算に対応しています。
使い方は、はじめに中央上のフォームに、計算式をアルファベットで入力します。
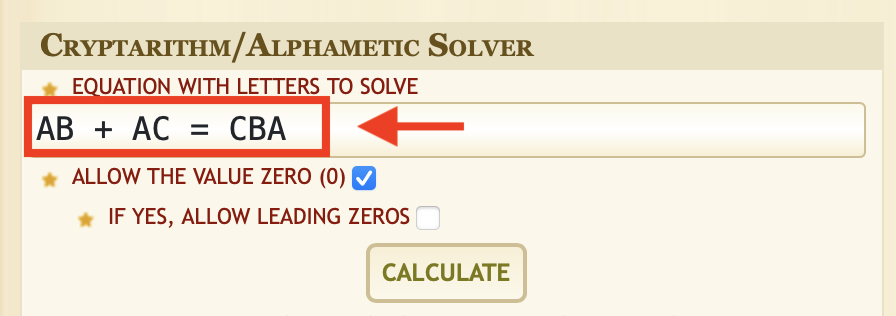
このとき、同じ文字が同じアルファベットになるように入力します。
入力したらすぐ下の「CALCULATE」ボタンを押します。
すると、画面左側に結果が表示されます。
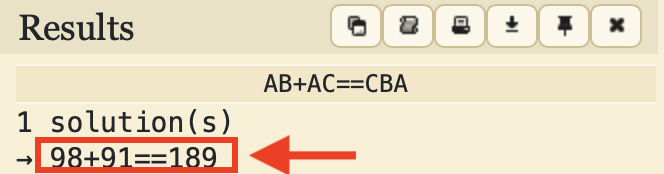
また、答えがない場合は「0 solution」、複数ある場合はすべて表示してくれます。
ちなみにこの「98+91=189」が冒頭で出した例題の答えです。
②作るときのルール
次に「覆面算」を作るときのルールを説明していきます。
ルールといっても、これを満たさないとそもそも計算式として成り立ちません。
- 同じ文字（または記号）には同じ数字が入ること
- 文字は10種類まで
- 足し算の結果は、足している数の桁数+1まで
（3桁+3桁=3桁 or 4桁にしかならない） - 一番上の位に0は入らない
どのルールも当たり前に思えますが、文字や記号で作っていると、突然文字が11種類になったりするので要注意です。
③作るときの手順
ここからは実際に「覆面算」を作るときの手順をお伝えします。
手順は次の通りです。
（１）任意の文字（または記号）で計算式を作る
↓
（２）サイトで一意解になるか検証する
↓
（３）一意解にならなかった場合
順番に説明していきます。
（１）任意の文字で計算式を作る
まず、数字は０〜９までなので、最大１０種類の文字で計算式を作っていきましょう。
謎解きに何かしらのテーマが用意されていれば、そのテーマに沿った「単語」だと、なお謎解きとしての面白味は増しますが、必須ではないので無理はしなくて大丈夫です。
任意の文字列で全然問題ありませんが、ここでは、有名な覆面算の問題でもある「バナナ＋バナナ＝シナモン」という文字列で作ったことにして次の手順に進みます。
（２）一意解になるかサイトで検証する
一意解とは「答えが一つに絞られる」ということです。
それでは先ほど紹介したサイトで「バナナ＋バナナ＝シナモン」が一意解になるか検証してみましょう。
サイトには同じ文字が同じアルファベットになるように「ABB+ABB=CBDE」と入力します。
その結果は以下の通り。
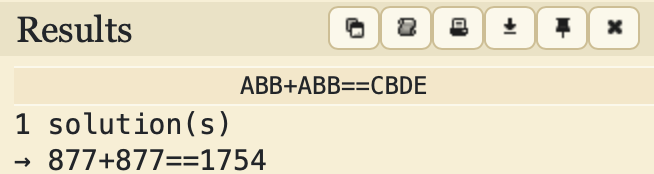
1 solutionということで、しっかり「一意解であること」が検証されました。
（この問題がなぜ有名なのかというと「バナナ＝８７７」でちょっとオシャレだからですね）
こんな感じで「一意解であること」が分かれば、ひとまず覆面算は完成です。
（３）一意解にならなかった場合
しかし、そうそう簡単に一意解にはなりません。むしろ、一意解にならない場合のほうが多いです。
試しに「ミカン＋ミカン＝ビタミン」が一意解になるかどうかサイトで検証してみます。
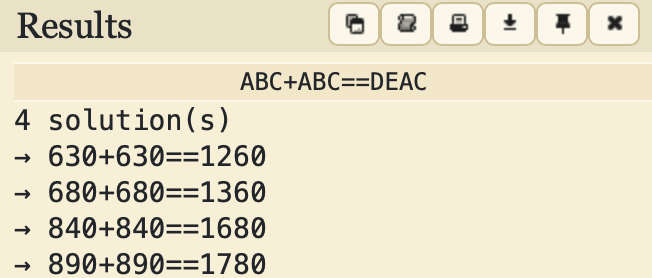
すると「4通りの結果」が表示されてしまいました。
このままでは覆面算としては使えませんが、ここにひと工夫加えることで、謎解きにすることができます。
それは「条件付きの覆面算にする」という方法です。
「条件付きの覆面算」では、上の4通りの結果の中から「どれか１桁を固定して、無理やり一意解にする」ことをいいます。
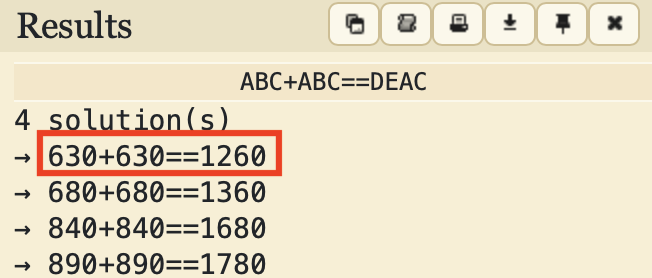
今回の結果なら、十の位を「3」に固定すれば、赤枠しかないので「一意解」となります。
つまり「ミカン＋ミカン＝ビタミン」かつ「カ＝３のとき」という問題にしてしまえば、覆面算として成立させることができます。
また、この問題の面白いところは「カ＝３のとき」と「カ＝４のとき」で答えが変わることです。
序盤では「カ＝３」で解かせて、終盤で「カ＝４」と条件を変化させることで「解き直しをさせる」なんて仕掛けにも使うこともできます。
３．謎解きを作ってみよう
それでは実際に「覆面算」を作る練習をしてみましょう。
【練習問題①】
次の覆面算は解けるでしょうか？
（１）AB＋CD＝EFGH
（２）LION+CATS=TIGER
【解答①】
どちらも解けない
（１）２桁＋２桁＝４桁になっている
（２）文字が１１種類使われている
練習問題①は「覆面算のルール」をしっかり確認する問題でした。
つづいてはこちら。
[練習問題②]
「AB+AC＝CBA」は一意解になることが分かっています。
AB,AC,CBAがそれぞれ単語となるように、A,B,Cに文字を入れてください。
【解答②】
カン(缶)＋カキ(柿)＝キンカ(金貨)
リス(栗鼠)＋リク(陸)＝クスリ(薬) など
この問題は、すでに出来上がっている覆面算に単語をあてはめる練習でした。解答例以外にもぴったりあう単語があれば、「SEND+MORE=MONEY」のような覆面算を作ることもできるかもしれません。
最後にもう１問。
【練習問題③】
「ABC+ABC=BCD」には複数の答えがあることが分かっています。
Aをいくつに固定すれば、一意解になるでしょうか？
【解答③】
「A=2」にすると「249+249=498」で一意解になる。
ほかに成立する式は以下の通り。
「124+124=248」
「125+125=250」
「374+374=748」
「375+375=750」
「A=1 または 3」では一意解にはならない。
この問題は、実際に検証サイトに「ABC+ABC=BCD」と入れると、すぐに答えが分かるようになっていました。
「覆面算」は計算に自信がある人であれば、頭の中や手計算で問題を考えることもできますが、思いがけないバグを防ぐためにも、また検算用にも、是非検証サイトを活用することをオススメします。
まとめ
ここまで「覆面算」の作り方をお伝えしてきました。
以下、まとめです。
- 覆面算を検証できるサイトが便利
- 一意解になるか確認する
- 複数の答えになっても「条件付き」で一意解にできる
「覆面算」は作るのも解くのも、少し手間がかかる問題ですが、定番の謎解きの中では大きく外れないジャンルの一つです。
もし今後、たくさんの小問を作る機会があれば、そのうちの１問をこの「覆面算」にしてみてはいかがでしょうか。その際は、是非この記事で紹介した方法で作ってみてください。
今回の記事は以上です。
ここまで読んでいただき、ありがとうございました！
